大话数据结构 读书笔记

🌳1. 绪论

🌳逻辑结构

  • 集合结构
  • 线性结构
  • 树形结构
  • 图形结构

🌳物理结构

  • 顺序存储结构
  • 链接存储结构

🌳2. 算法

🌳算法特征

  • 输入输出
  • 有穷性
  • 确定性
  • 可行性

🌳算法时间复杂度

🌳常数阶 O(1)

🌳线性阶 O(n)

🌳对数阶 O(logn)

1
2
3
4
5
int count =1;
while(count < n)
{
    count = count * 2;
}

2x=n=>x=log2n{2^x} = n => x = log_2n

🌳平方阶 O(n2)O({n^2})

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int i,j;
for (i = 0; i < m; i++)
{
    for (j= 0; j < n; j++)
    {
    /* 时 间 复 杂 度 为 0(1) 的 程序 步骤 序 列 */
    }
}

int i,j;
for(i = 0; i <n; i++)
{
for (j =i; j <n; j++) /* 注意j = i 而不 是0 */
{
/* 时间 复 杂 度为0(1) HBRP RAR */
}
}

n+(n−1)+(n−2)+⋯+1=n(n+1)2=n22+n2n+(n-1)+(n-2)+{\cdots}+1 =\frac{n(n+1)}{2}=\frac{n^2}{2}+\frac{n}{2}

O(n2)O(n^2)

🌳常见时间复杂度

O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)< O(n!) < O(n^n)

🌳3. 线性表

🌳随机存取结构

那 么 我们 对 每个线性 表 位 置 的 存入或者取出 数据,对于计算机 来说 都是相等的时间,
也 就 是 一 个 常数,它 的存取 时间人性能为O(1)。
我们 通常 把具有 这 一 特点 的 存储 结构 称为随机存取结构

线性 表 的 顺序 存储 结构,在 存、读 数据 时,不 管 是 哪个 位 置 ,时间
复杂度 都是 O(1); 而 插入 或 删除 时,时间 复 杂 度 都是 O(n)。

🌳线性 表 链 式 存储 结构 单 链表

在 单链表 的 第一个 结点前 附设 个 结 点,称 为头结 点 。\头 结 点 的 数据 域可以 不 存储 任何信息,
也可以 存储如 线性 表 的 长 度 等附加 信息,头 结 点 的 指针 域存储 指向 第 一 个结 点 的指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType; // 定义数据元素类型
typedef int Status;   // 定义状态类型
#define OK 1
#define ERROR 0

// 定义单链表的节点结构
typedef struct Node {
    ElemType data;       // 数据域
    struct Node *next;   // 指针域，指向下一个节点
} Node, *LinkList;

// 单链表插入操作
Status ListInsert(LinkList *L, int i, ElemType e) {
    int j = 1; // 计数器，表示当前节点的位置
    LinkList p, s;
    p = *L; // p指向链表的头节点

    // 寻找第i-1个节点
    while (p && j < i) {
        p = p->next;
        j++;
    }

    // 如果第i-1个节点不存在，则返回错误
    if (!p || j > i) {
        return ERROR;
    }

    // 创建新节点
    s = (LinkList)malloc(sizeof(Node));
    if (!s) {
        return ERROR; // 内存分配失败
    }

    s->data = e;       // 将数据赋值给新节点
    s->next = p->next; // 将p的后继节点赋值给新节点的后继
    p->next = s;       // 将新节点插入到p之后

    return OK;
}

// 测试单链表插入操作
int main() {
    LinkList L = (LinkList)malloc(sizeof(Node)); // 创建头节点
    L->next = NULL;                              // 初始化为空链表

    // 插入元素
    ListInsert(&L, 1, 10);
    ListInsert(&L, 2, 20);
    ListInsert(&L, 3, 30);

    // 遍历链表
    LinkList p = L->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType; // 定义数据元素类型
typedef int Status;   // 定义状态类型
#define OK 1
#define ERROR 0

// 定义单链表的节点结构
typedef struct Node {
    ElemType data;       // 数据域
    struct Node *next;   // 指针域，指向下一个节点
} Node, *LinkList;

// 单链表删除操作
Status ListDelete(LinkList *L, int i, ElemType *e) {
    int j = 1; // 计数器，表示当前节点的位置
    LinkList p, q;
    p = *L; // p指向链表的头节点

    // 寻找第i-1个节点
    while (p && j < i) {
        p = p->next;
        j++;
    }

    // 如果第i-1个节点不存在或i无效，则返回错误
    if (!p || !(p->next)) {
        return ERROR;
    }

    q = p->next;       // q指向要删除的节点
    *e = q->data;      // 将删除节点的数据赋值给e
    p->next = q->next; // 将q的后继节点赋值给p的后继
    free(q);           // 释放q节点的内存

    return OK;
}

// 测试单链表删除操作
int main() {
    LinkList L = (LinkList)malloc(sizeof(Node)); // 创建头节点
    L->next = NULL;                              // 初始化为空链表

    // 插入一些元素
    LinkList p = L;
    for (int i = 1; i <= 5; i++) {
        LinkList newNode = (LinkList)malloc(sizeof(Node));
        newNode->data = i * 10;
        newNode->next = NULL;
        p->next = newNode;
        p = newNode;
    }

    // 删除第3个节点
    ElemType e;
    if (ListDelete(&L, 3, &e) == OK) {
        printf("删除成功，删除的元素是: %d\n", e);
    } else {
        printf("删除失败\n");
    }

    // 遍历链表
    p = L->next;
    printf("链表中的元素: ");
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }

    return 0;
}

时间 复 杂 度 都是 O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType; // 定义数据元素类型
typedef int Status;   // 定义状态类型
#define OK 1
#define ERROR 0

// 定义单链表的节点结构
typedef struct Node {
    ElemType data;       // 数据域
    struct Node *next;   // 指针域，指向下一个节点
} Node, *LinkList;

// 尾插法创建单链表
Status CreateList(LinkList *L, int n) {
    *L = (LinkList)malloc(sizeof(Node)); // 创建头节点
    if (!(*L)) return ERROR;             // 内存分配失败
    (*L)->next = NULL;                   // 初始化为空链表

    LinkList tail = *L; // 尾指针，初始指向头节点
    for (int i = 1; i <= n; i++) {
        LinkList newNode = (LinkList)malloc(sizeof(Node)); // 创建新节点
        if (!newNode) return ERROR;                       // 内存分配失败
        printf("请输入第 %d 个元素的值: ", i);
        scanf("%d", &newNode->data); // 输入数据
        newNode->next = NULL;        // 新节点的指针域置为空
        tail->next = newNode;        // 将新节点链接到链表尾部
        tail = newNode;              // 更新尾指针
    }
    return OK;
}

// 遍历单链表
void TraverseList(LinkList L) {
    LinkList p = L->next; // 跳过头节点
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

// 测试整表创建
int main() {
    LinkList L;
    int n;

    printf("请输入链表的长度: ");
    scanf("%d", &n);

    if (CreateList(&L, n) == OK) {
        printf("链表创建成功，链表中的元素为: ");
        TraverseList(L);
    } else {
        printf("链表创建失败\n");
    }

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType; // 定义数据元素类型
typedef int Status;   // 定义状态类型
#define OK 1
#define ERROR 0

// 定义单链表的节点结构
typedef struct Node {
    ElemType data;       // 数据域
    struct Node *next;   // 指针域，指向下一个节点
} Node, *LinkList;

// 整表删除操作
Status ClearList(LinkList *L) {
    LinkList p, q;
    p = (*L)->next; // 指向头节点的下一个节点
    while (p) {
        q = p->next; // 保存下一个节点
        free(p);     // 释放当前节点
        p = q;       // 移动到下一个节点
    }
    (*L)->next = NULL; // 将头节点的指针域置为空
    return OK;
}

// 测试整表删除操作
int main() {
    LinkList L = (LinkList)malloc(sizeof(Node)); // 创建头节点
    L->next = NULL;                              // 初始化为空链表

    // 插入一些元素
    LinkList p = L;
    for (int i = 1; i <= 5; i++) {
        LinkList newNode = (LinkList)malloc(sizeof(Node));
        newNode->data = i * 10;
        newNode->next = NULL;
        p->next = newNode;
        p = newNode;
    }

    // 遍历链表
    printf("链表中的元素: ");
    p = L->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");

    // 删除整表
    if (ClearList(&L) == OK) {
        printf("链表已清空\n");
    } else {
        printf("链表清空失败\n");
    }

    // 再次遍历链表
    printf("链表中的元素: ");
    p = L->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");

    return 0;
}

。 比 如 说 游戏 开发 中 ,
对 于 用 户 注册 的 个 人 信息 , 除 了 注册 时 插入 数据 外, 绝 大 多 数 情况 都 是 读
取 , 所 以 应 该 考虑 用 顺序 存储 结构。而 游戏 中 的 玩家 的 武器 或 者 装备 列
表 , 随 着 玩家 的 游戏 过 程 中 , 可 能 会 随时 增加 或 删除 , 此 时 再 用 顺序 存储
就 不 太 合适 了 , 单 链表 结构 就 可 以 大 展 拳

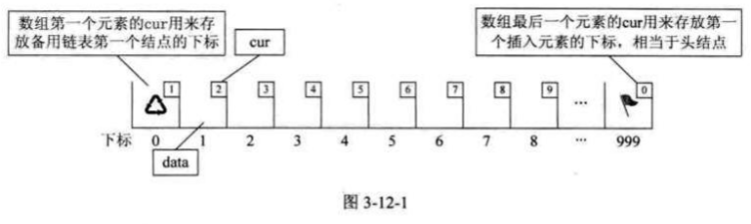
🌳静态链表

用 数组描述 的 链表叫做 静态链表,这 种 描述 方法还有 起 名叫做 游标 实Wik.

静态链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <stdio.h>

#define MAXSIZE 1000 // 静态链表的最大长度
#define ERROR 0
#define OK 1
typedef int Status;
typedef int ElemType;

// 定义静态链表的节点结构
typedef struct {
    ElemType data; // 数据域
    int cur;       // 游标，指向下一个节点的位置
} Component, StaticLinkList[MAXSIZE];

// 初始化静态链表
Status InitList(StaticLinkList space) {
    for (int i = 0; i < MAXSIZE - 1; i++) {
        space[i].cur = i + 1; // 将每个节点的游标指向下一个节点
    }
    space[MAXSIZE - 1].cur = 0; // 最后一个节点的游标为0，表示空
    return OK;
}

// 分配节点
int Malloc_SLL(StaticLinkList space) {
    int i = space[0].cur; // 获取备用链表的第一个节点
    if (i) {
        space[0].cur = space[i].cur; // 更新备用链表的头节点
    }
    return i;
}

// 插入操作
Status ListInsert(StaticLinkList L, int i, ElemType e) {
    if (i < 1 || i > MAXSIZE - 1) {
        return ERROR; // 插入位置不合法
    }
    // 数组最后一个元素的cur用来存放第一个插入元素的下标
    int k = MAXSIZE - 1; // k指向头节点
    for (int j = 1; j < i; j++) {
        //这里的k 意味着 第j个元素的cur的值
        k = L[k].cur; // 找到第i-1个节点
        if (k == 0) {
            return ERROR; // 如果节点不存在，返回错误
        }
    }
    int newNode = Malloc_SLL(L); // 分配一个新节点
    if (newNode) {
        L[newNode].data = e;       // 将数据赋值给新节点
        L[newNode].cur = L[k].cur; // 新节点的游标指向第i个节点
        L[k].cur = newNode;        // 第i-1个节点的游标指向新节点
        return OK;
    }
    return ERROR; // 分配失败
}

// 遍历静态链表
void TraverseList(StaticLinkList L) {
    int i = L[MAXSIZE - 1].cur; // 从头节点开始
    while (i) {
        printf("%d ", L[i].data);
        i = L[i].cur; // 移动到下一个节点
    }
    printf("\n");
}

// 测试静态链表插入操作
int main() {
    StaticLinkList L;
    InitList(L); // 初始化静态链表

    // 插入元素
    ListInsert(L, 1, 10);
    ListInsert(L, 2, 20);
    ListInsert(L, 3, 30);

    // 遍历链表
    printf("静态链表中的元素: ");
    TraverseList(L);

    return 0;
}

🌳循环链表

将 单 链表 中 终端 结 点 的 指针 端由空 指针 改 为指向 头 结 点 ,就 使 整个单 链表 形成一个环,这 种头尾 相 接 的 单链表 称 为 单 循环链表,简 称 循环链表 (circular linkedlist).

循环链表使用尾指针 这样就知道 头结点跟尾节点的指针
如果使用头指针 就无法直接定位尾节点

循环链表的合并

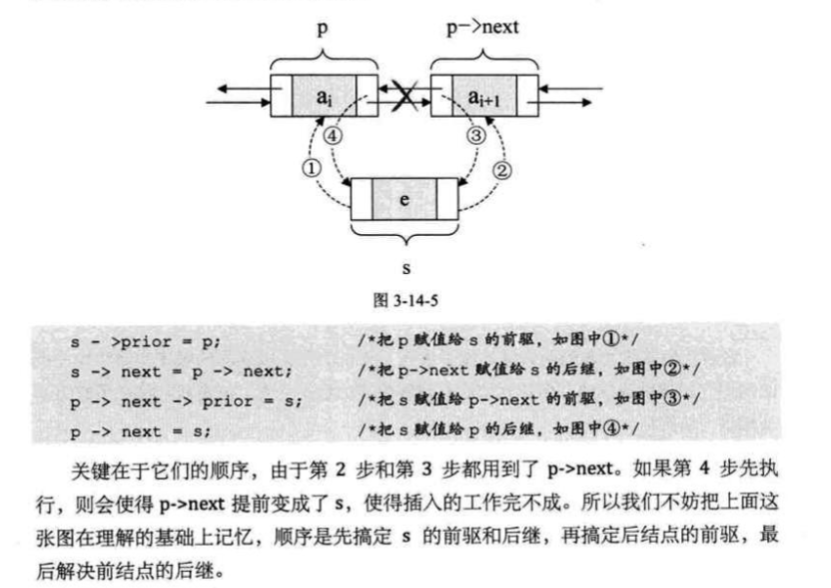
🌳双向链表

双向链表插入赋值顺序

🌳4. 栈与队列

🌳栈 last in first out LIFO

🌳栈的顺序存储结构与实现

🌳两栈共享空间

🌳栈的链式存储结构与实现

🌳栈的应用 四则运算表达式 中缀表达式转后缀表达式

🌳队列 first in first out FIFO

🌳循环队列 解决假溢出

🌳队列的链式存储结构

🌳5. 字符串

🌳KMP模式匹配

kmp算法

🌳6. 树

判断一个结构是不是树，通常需要满足以下几个条件：

  1. 连通性：所有节点都是连通的，即任意两个节点之间都有路径相通。
  2. 无环性：结构中不能有回路（环），即不存在从某个节点出发经过若干条边又回到自身的路径。
  3. n个节点有n-1条边：对于有n个节点的无向图，如果它是树，则恰好有n-1条边。
  4. 唯一根节点（有向树）：对于有向树（如二叉树），有且只有一个入度为0的节点（根节点），其余节点入度为1。

总结：
树是一种连通且无环的图结构，并且边数等于节点数减一。

判断方法举例（以无向图为例）：

  • 用深度优先搜索（DFS）或广度优先搜索（BFS）遍历，看是否所有节点都能访问到（连通），且遍历过程中不出现回到已访问节点的情况（无环）。
  • 检查边数是否为n-1。

伪代码示例：

1
2
3
4
5
6
7
// 判断无向图是否为树
bool isTree(Graph g) {
    if (!isConnected(g)) return false;
    if (hasCycle(g)) return false;
    if (g.edgeCount != g.nodeCount - 1) return false;
    return true;
}

🌳概念

结 点拥有 的 子树数 称为结点 的度(Degree)。
度为0 的 结 点 称为叶 结点〈Leaf) 或终端结点;
度 不为 0 的 结 点称 为非 终端结点 或 分 支 结 点。除 根 结 点 之 外,分 支 结 点 也称为 内 部 结 点。
树 的 度 是 树内 各 结 点 的 度 的 最 大值

如 果 将 树 中 结 点 的 各 子 树 看 成从左 至 右 是有次 序 的 ,不 能 互 换 的 ,则 称 该 树 为有序树,否 则 称 为 无 序树

二叉树(Binary Tree) 是 n (n>0 ) 个 结 点的有 限 集合,该集合
或者为空集 ( 称 为 空二叉树), 或者由 一 个 根 结点和 两 棵 互不相交
的、分 别称 为 根结点的左 子树和 右 子 树的二 叉 树组 成

左斜树
右斜数
满二叉树

对一棵具有 n 个结点 的 二 叉 树按层 序 编号,如 果编号为1 (1<i<n)(1<i<n) 的 结 点与同样深度 的 满 二又树 中 编号为1 的 结 点 在二叉 树 中 位 置完全 相同,则 这棵二叉树称为 完全二叉树，编号是连续的

🌳性质

完全二叉树 结点度为1 则该结点只有左孩子 不存在只有右子树的情况

同样结点数的二叉树 完全二叉树深度最小

n0n_0 终端结点数
n1n_1 度=1结点数 有一分支
n2n_2 度=2结点数 有两分支
n 总结点数

n=n0+n1+n2n = n_0 + n_1 + n_2

二叉树：分支数 = 总结点数-1

n1∗1+n2∗2=n−1n_1*1 + n_2*2 = n-1

∴ $$ n_0 + n_1 + n_2 - 1 = n_11 + n_22 $$
∴ $$ n_0 = n_2 + 1 $$

即 终端结点数 = 2度结点数 + 1

二叉树 第i层至多有 2i−12^{i-1} 个结点 i ≥ 1

深度为k的二叉树至多有 2k−12^k-1 个结点 i ≥ 1

n个结点的满二叉树 n=2k−1n=2^k-1 深度为 k=log2(n+1)k=log_2(n+1)

🌳完全二叉树结点数

  • ≤ 同度数满二叉树 2k−12^k-1
  • ＞ 2k−1−12^{k-1}-1

∴ $ 2^{k-1}-1 < n ≤ 2^k-1 $

  • n 是整数 ∴ n≤2k−1n ≤ 2^k-1 => n<2kn<2^k
  • n 是整数 ∴ n>2k−1−1n > 2^{k-1}-1 => n≥2k−1n ≥ 2^{k-1}
    ∴ $ 2^{k-1} ≤ n < 2^k $
    ∴ $ k-1 ≤ log_2n < k $
    ∵ k作为度数是整数 例子: 5≤x<65 ≤ x < 6 ∴ x ≈ 5.u ∴ 对x取整 + 1 = k
    ∴ k=⌊log2n⌋+1k = ⌊log_2n⌋ + 1
1
2
3
设x是一个实数，则x可以表示为整数部分和小数部分的和，即x = ⌊x⌋ + {x}，其中⌊x⌋是x的整数部分，{x}是x的小数部分
上取整 (Ceiling)：用数学符号⌈x⌉表示，表示大于等于x的最小整数。例如，⌈4.2⌉=5，⌈-4.2⌉=-4。
下取整 (Floor)：用数学符号⌊x⌋表示，表示小于等于x的最大整数。例如，⌊4.2⌋=4，⌊-4.2⌋=-5。

n结点完全二叉树 (深度为⌈log2n⌉+1⌈log_2n⌉ + 1) 任一结点 i：

  • i = 1, i为根, i>1, parent= ⌊i/2⌋
  • 2i > n, i 无左孩子 否则 Lchild = 2i
  • 2i+1 > n, i 无右孩子 否则 Rchild = 2i+1

🌳二叉树存储结构

🌳顺序存储一般只用于 完全二叉树

🌳二叉链表

🌳遍历二叉树

  • 前序遍历 根-左树全左后回溯时顺便访问右结点-右树全左后回溯时顺便访问右结点

  • 中序遍历 左树最左结点开始-回溯时顺便访问右结点右叶子-根结点-右树最左结点开始-回溯时顺便访问右结点右叶子

  • 后序遍历 左树最底层叶子开始-回溯时从下到上从左到右访问左树节点-右树最底层叶子开始-回溯时从下到上从左到右访问右树节点-根

  • 层序遍历 根-从上到下从左到右一层一层遍历

  • 前序遍历+中序遍历 唯一确定二叉树

  • 后序遍历+中序遍历 唯一确定二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
// ...existing code...
typedef struct BiTNode {
    char data;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

// 前序遍历：根-左-右
void PreOrder(BiTree T) {
    if (T) {
        printf("%c ", T->data);      // 访问根节点
        PreOrder(T->lchild);         // 遍历左子树
        PreOrder(T->rchild);         // 遍历右子树
    }
}

// 中序遍历：左-根-右
void InOrder(BiTree T) {
    if (T) {
        InOrder(T->lchild);          // 遍历左子树
        printf("%c ", T->data);      // 访问根节点
        InOrder(T->rchild);          // 遍历右子树
    }
}

// 后序遍历：左-右-根
void PostOrder(BiTree T) {
    if (T) {
        PostOrder(T->lchild);        // 遍历左子树
        PostOrder(T->rchild);        // 遍历右子树
        printf("%c ", T->data);      // 访问根节点
    }
}

// 层序遍历算法（使用队列）
void LevelOrder(BiTree T) {
    if (!T) return;
    // 简单队列实现
    BiTree queue[100];
    int front = 0, rear = 0;
    queue[rear++] = T;
    while (front < rear) {
        BiTree node = queue[front++];
        printf("%c ", node->data); // 访问当前节点
        if (node->lchild) queue[rear++] = node->lchild;
        if (node->rchild) queue[rear++] = node->rchild;
    }
}
// ...existing code...
🌳例子1

前序序列：ABCDEFGH
中序序列：CDBAFEHG

前序第一个节点必为根

🌳例子2

后序序列：GDBEFCA
中序序列：DGBAECF

∵ 后序 最后一个必为根 A=根
∴ 中序序列中 DGB为左子树 ECF为右子树
∵ 中序序列根结点左边第一个必为根的左子树 所以 B为根左结点
后序遍历 G在D前面 所以
要么GD都为 B得子节点
要么G是D的子节点 D是B的子节点
但是中序遍历中先访问的D再访问G 如果GD都是B子节点 后序遍历左子树应该是DGB 矛盾
∴确定左子树
∵存在跟左右子树的情况下 后序遍历倒数第二个必为根的右子树节点 C为根左节点
∴

  • EF要么是C的子节点
  • 要么E是F的子节点
    ∵ 中序遍历中 右子树ECF E为第一个 C比F先遍历
    ∴ E是C的子节点 E,F没有父子关系
    ∴ F是C的子节点
    ∴确定右子树

🌳扩展二叉树 建树

前序遍历：AB#D##C##

🌳树 森林 二叉树的 转换

🌳树 -> 二叉树

  • 兄弟加线
  • 保留每个结点第一个子节点连线 其他删除
  • 层次调整 第一个子节点为左孩子 兄弟转换过来的为右孩子

🌳森林 ->

  • 树转二叉树
  • 树根做另一棵树根节点的右孩子

🌳二叉树 -> 树

  • 所有左孩子的右子结点连接其父节点的父节点(爷爷节点)
  • 删除右子节点原来的与其父节点连线

🌳二叉树 -> 森林

  • 砍根结点的右分支 根节点右孩子子树独立

🌳树遍历

  • 先根遍历
  • 后根遍历

🌳森林遍历

  • 前序遍历
  • 后序遍历

🌳前驱后继 线索二叉链表 线索二叉树 threaded binary tree

🌳赫夫曼树

带劝路径长度 WPL 最小的二叉树

设计长 短 不 等 的编码,则 必须是任 一 字符 的编码 都 不 是另一 个 字符 的 编码的 前缀 ,这 种编码称做前缀编码

赫夫曼编码
字符集 d1,d2,⋯,dn{d_1,d_2,{\cdots},d_n} -> 叶子
字符频率 w1,w2,⋯,wn{w_1,w_2,{\cdots},w_n} -> 叶子权值
构造赫夫曼树
左分支代表0 右分支代表1
叶子结点路径的分支01序列为该叶子字符的编码

🌳7. 图

🌳概念

图中数据元素 -> 顶点 vertex
有穷非空
无向边 无向图 (A,D) (D,A)
有向边 弧 <A, D>
简单图：不存在顶点到自身的边 同一条边不重复出现
无向完全图：任意两顶点都存在边 $ e = \frac{n*(n-1)}{2}$
有向完全图：任意两顶点都存在方向互为相反的两条弧 $ e = n*(n-1)$
稀疏图：有很少边或弧的图
稠密图
权 weight：与图的边或弧相关的数
网：带权的图
子图

V表示顶点集合
{E}表示边/弧 集合
无向图G=(V,{E}) 边(v,v’) ∈ E => v,v’互为邻接点(adjacent)
顶点v的度(Degree) : TD(v) = v的邻接边数
图总边数: $ e = \frac{1}{2}\sum_{i=1}^nTD(v_i) $

有向图G=(V,{E}) 弧 <v,v′>∈E<v,v'> ∈ E => v,v’邻接到顶点v’
顶点v的入度(InDegree) : ID(v) = v为弧头的弧数
顶点v的出度(OutDegree) : OD(v) = v为弧尾的弧数
TD(v)=ID(v)+OD(v)
图总边数: e=∑i=1nID(vi)=∑i=1nOD(vi)e = \sum_{i=1}^nID(v_i) = \sum_{i=1}^nOD(v_i)

路径长度 = 路径(边/弧)数
回路/环：首尾顶点相同的路径
简单路径
简单 环/回路 B-C-A-D-B 除首尾顶点 其余顶点不重复
B-C-D-A-C -> 不是简单环
无向图中 v到v’有路径 则v和v’是连通的
连通图：任意两顶点都连通 则该图为连通图(Connected Graph)
连通分量：无向图中的极大连通子图
强连通图：在有向图中,每一对 vi,vj∈Vv_i,vj∈V、vi≠vjv_i≠v_j, 从viv_i到vjv_j,从vjv_j到viv_i 都有路径
强连通分量: 有向图中的极大强连通子图称
连通图生成树：一个极小的连通子图 包含全部n个顶点 只有构成树🌳的n-1条边
非连通图：n个顶点 边 e < n-1
n个顶点的图 边 e > n-1 图必定有环
有向树：图有一个顶点 入度=0 其余顶点 入度均=1(只有一个父节点)
生成树：无向图中连通且 n个顶点n-1条边
生成森林：有向图分解成若干棵有向树构成生成森林

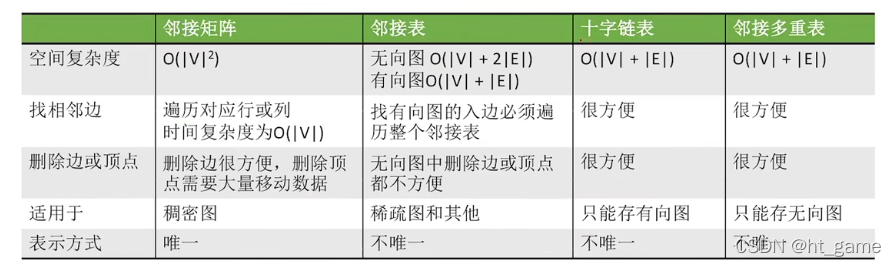
🌳存储结构

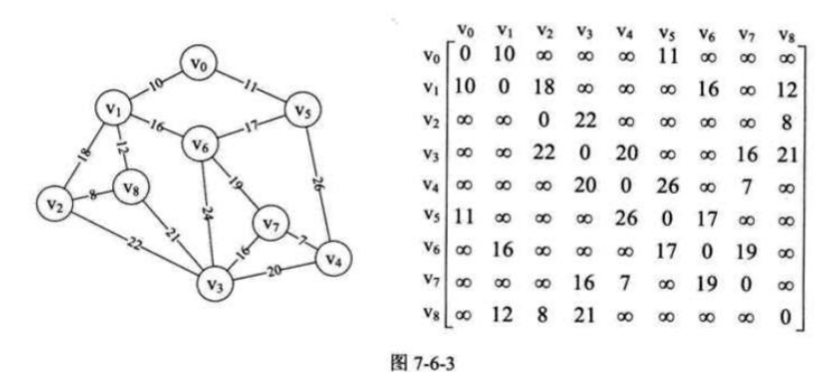
🌳邻接矩阵

无向图边数组是一个对称矩阵
两个数组表示图

  • 一维数组 存储 顶点
  • 二维数组存储 边/弧
🌳无向图/有向图 邻接矩阵

顶点数组：
v0v1v2v3 \begin{array}{|c|c|c|c|} \hline v_0 & v_1 & v_2 & v_3 \\ \hline \end{array}

边数组：

↓v0v1v2v3v0v1v2v30111101011011010 \begin{array}{c|c} \color{lime}{↓}& \color{yellow}\begin{matrix} v_0 & v_1 & v_2 & v_3 \\ \end{matrix} \\ \hline \color{teal} \begin{matrix} v_0 \\ v_1 \\ v_2 \\ v_3 \\ \end{matrix} & \color{fuchsia} \begin{matrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{matrix} \end{array}

🌳网 邻接矩阵

顶点数组：
v0v1v2v3v4 \begin{array}{|c|c|c|c|c|} \hline v_0 & v_1 & v_2 & v_3 & v_4 \\ \hline \end{array}

边数组：
↓v0v1v2v3v4v0v1v2v3v40∞∞∞6903∞∞2∞05∞∞∞∞01∞∞∞∞0 \begin{array}{c|c} \color{lime}{↓}& \color{yellow}\begin{matrix} v_0 & v_1 & v_2 & v_3 & v_4 \\ \end{matrix} \\ \hline \color{teal} \begin{matrix} v_0 \\ v_1 \\ v_2 \\ v_3 \\ v_4 \\ \end{matrix} & \color{fuchsia} \begin{matrix} 0 & ∞ & ∞ & ∞ & 6 \\ 9 & 0 & 3 & ∞ & ∞ \\ 2 & ∞ & 0 & 5 & ∞ \\ ∞ & ∞ & ∞ & 0 & 1 \\ ∞ & ∞ & ∞ & ∞ & 0 \\ \end{matrix} \end{array}

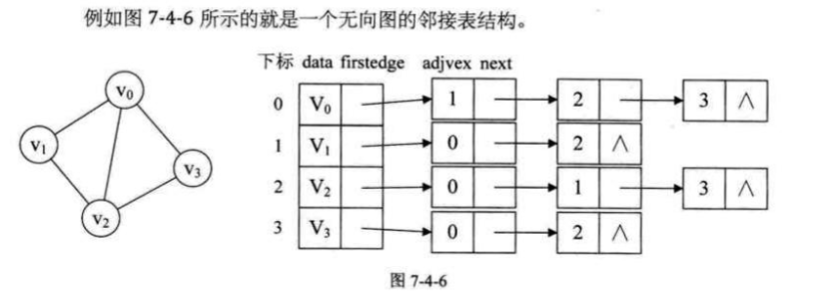
🌳邻接表

顶点少 稀疏图 邻接图存储结构 浪费空间

邻接表 adjacency List：数组+链表
无向图 -> 边表
有向图 -> 弧尾出边表
有向图逆邻接表 -> 弧头的表

邻接表

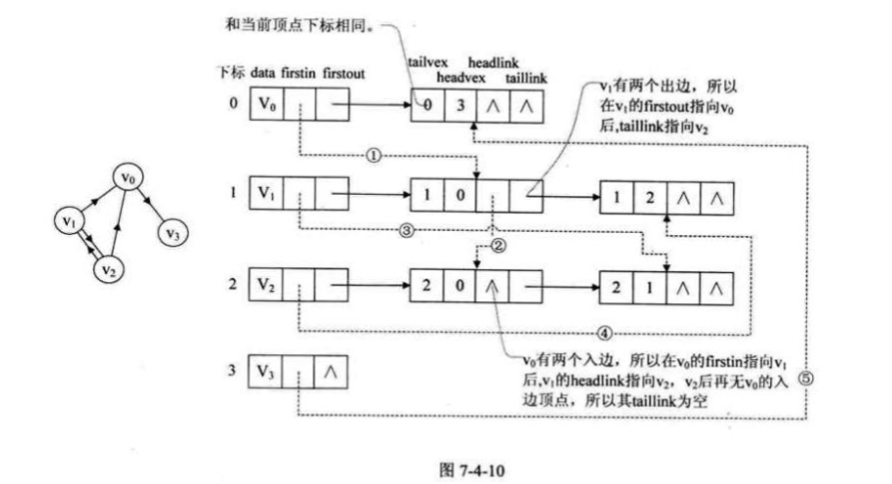
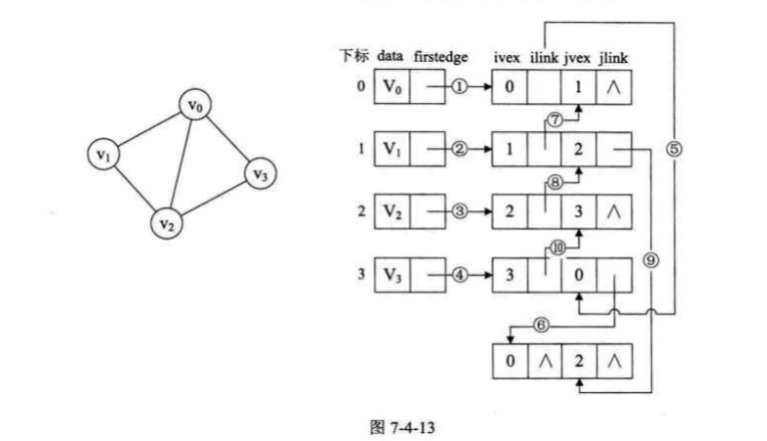
🌳十字链表

Orthogonal List

十字链表

🌳邻接多重表

邻接多重表

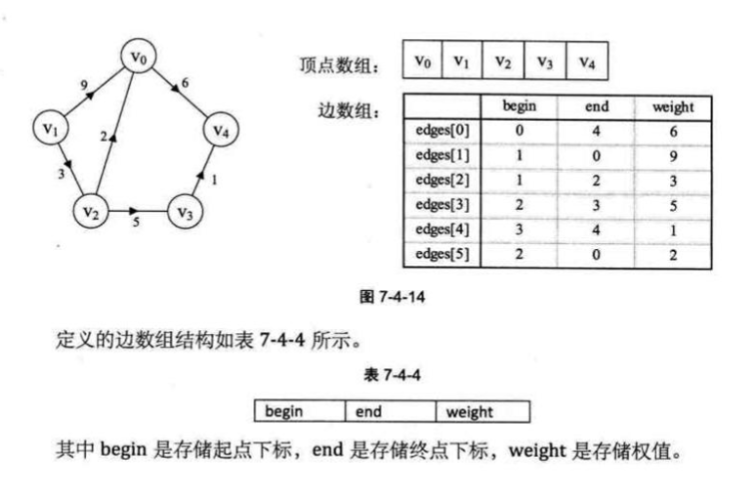
🌳边集数组

边集数组

结构特征对比

🌳图的遍历

traveling graph

🌳深度优先遍历

DFS depth first search

从图中 某个顶点v出发 然后从v的未被访问的邻接点出发深度优先遍历图
直至所有和v有路径相通的顶点都被访问到

🌳邻接矩阵 DFS
  • 遍历点数组
  • 查询点A 查询该点的边矩阵 访问该点的第一个邻接点B 然后标记已访问
  • 访问该邻接点B 查询该点的边矩阵 访问该点的第一个邻接点C 然后标记已访问
  • 访问C 。。。同理 直到该 分支点 全被访问结束
  • 回溯C 查询该点的其余未访问邻接点 全被访问结束
  • 回溯B … 直到回溯A
🌳邻接表
  • 遍历点数组
  • 对点A 访问该点的邻接链表 访问第一分支邻接点B 然后标记已访问
  • 查询B … 查询C
  • 回溯 C 回溯B 回溯A

深度遍历 类似前序遍历 选一分支往深度查询然后回溯 直到所有分支结束

🌳广度优先搜索

BFS breadth first search

图文详解两种算法：深度优先遍历（DFS）和广度优先遍历（BFS

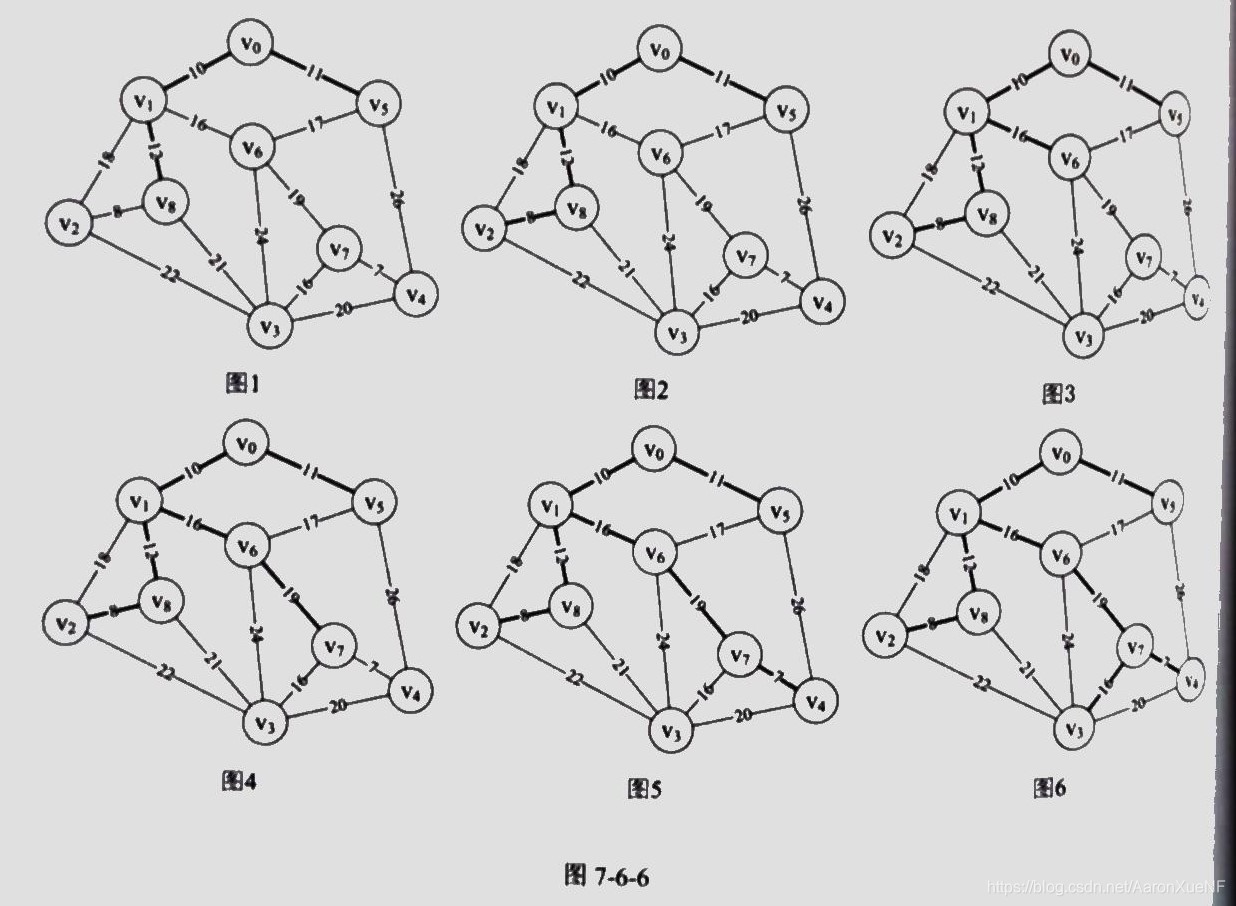
🌳最小生成树

minimum cost spanning tree

🌳prim 算法

prim算法

🌳adjvex数组

在 Prim算法 中用于存储 lowcost数组 每项权值对应的范围内顶点下标，主要用于输出最小生成树的边信息‌
在Prim算法中，adjvex数组记录了lowcost数组中每个最小权值对应的顶点下标，这样可以在生成最小生成树的过程中，通过adjvex数组确定每条边的起点和终点，从而输出最小生成树的边信息‌

具体来说，adjvex数组的作用包括：

-‌ 存储顶点下标‌：adjvex数组用于保存lowcost数组中每个最小权值对应的顶点下标。这样可以在生成最小生成树的过程中，通过adjvex数组确定每条边的起点。
‌- 输出边信息‌：在Prim算法中，通过遍历adjvex数组，可以输出构成最小生成树的边信息。
例如，当找到一个顶点的lowcost值最小且不为0时，可以通过adjvex数组确定该顶点的下标，从而输出对应的边信息‌

通过使用adjvex数组，Prim算法能够有效地构建连通网的最小代价生成树，确保生成的树是最小生成树。

🌳prim 算法原理
  • 从 v0v_0 开始 根据邻接矩阵 遍历 v0v_0 的邻接边
  • 记录📝v0v_0 到每个点(注意不是其邻接点是每个点)的最小边权值 lowcost
  • 取最小边权点 k 根据邻接矩阵 扫描该点 k 邻接边权值 并记录 lowcost
  • 再次取最小边权点 k … 重复 n-1次

适合用于稠密图

🌳prim 算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <stdio.h>
#include <stdlib.h>

#define MAXVEX 100
#define INFINITY 65535

typedef struct {
    int numVertexes;
    int arc[MAXVEX][MAXVEX];
} MGraph;

// Prim算法
void MiniSpanTree_Prim(MGraph G) {
    int min, i, j, k;
    int adjvex[MAXVEX];   // 保存相关顶点下标
    int lowcost[MAXVEX];  // 保存相关顶点间边的权值

    lowcost[0] = 0;       // 第一个顶点加入生成树
    adjvex[0] = 0;
    for (i = 1; i < G.numVertexes; i++) {
        lowcost[i] = G.arc[0][i];
        adjvex[i] = 0;
    }

    for (i = 1; i < G.numVertexes; i++) {
        min = INFINITY;
        k = 0;
        for (j = 1; j < G.numVertexes; j++) {
            if (lowcost[j] != 0 && lowcost[j] < min) {
                min = lowcost[j];
                k = j;
            }
        }
        printf("(%d, %d) 权值: %d\n", adjvex[k], k, min);
        lowcost[k] = 0;
        for (j = 1; j < G.numVertexes; j++) {
            if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) {
                lowcost[j] = G.arc[k][j];
                adjvex[j] = k;
            }
        }
    }
}

// 示例主函数
int main() {
    MGraph G;
    int i, j;
    G.numVertexes = 6;
    int arc[6][6] = {
        {0, 6, 1, 5, INFINITY, INFINITY},
        {6, 0, 5, INFINITY, 3, INFINITY},
        {1, 5, 0, 5, 6, 4},
        {5, INFINITY, 5, 0, INFINITY, 2},
        {INFINITY, 3, 6, INFINITY, 0, 6},
        {INFINITY, INFINITY, 4, 2, 6, 0}
    };
    for (i = 0; i < G.numVertexes; i++)
        for (j = 0; j < G.numVertexes; j++)
            G.arc[i][j] = arc[i][j];

    printf("最小生成树的边如下：\n");
    MiniSpanTree_Prim(G);
    return 0;
}

prim流程图

🌳辅助理解的参考资料

数据结构与算法 - 图 最小生成树（一）Prim算法

🌳kruskal 算法

  • 边集数组 存 边头尾边权
  • 按边权从小到大排序 边集数组
  • 遍历每条边 查询 并集/(有环)
  • 遍历完所有边就结束🔚

适用于稀疏图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <stdio.h>
#include <stdlib.h>

#define MAXVEX 100
#define MAXEDGE 100

typedef struct {
    int begin;
    int end;
    int weight;
} Edge;

typedef struct {
    int numVertexes, numEdges;
    int vexs[MAXVEX];
    int arc[MAXVEX][MAXVEX];
} MGraph;

typedef struct {
    int parent[MAXVEX];
    int n;
} DisjointSet;

// 查找根节点
int Find(DisjointSet *ds, int f) {
    while (ds->parent[f] > 0)
        f = ds->parent[f];
    return f;
}

// 合并集合
void Union(DisjointSet *ds, int i, int j) {
    int root1 = Find(ds, i);
    int root2 = Find(ds, j);
    if (root1 != root2)
        ds->parent[root2] = root1;
}

// 边排序
void SortEdges(Edge edges[], int numEdges) {
    int i, j;
    Edge temp;
    for (i = 0; i < numEdges - 1; i++) {
        for (j = 0; j < numEdges - 1 - i; j++) {
            if (edges[j].weight > edges[j + 1].weight) {
                temp = edges[j];
                edges[j] = edges[j + 1];
                edges[j + 1] = temp;
            }
        }
    }
}

// Kruskal 算法
void Kruskal(MGraph G) {
    int i, n, m;
    Edge edges[MAXEDGE];
    int k = 0;
    DisjointSet ds;
    int sum = 0;

    // 初始化并查集
    for (i = 0; i < G.numVertexes; i++)
        ds.parent[i] = 0;

    // 提取所有边
    for (i = 0; i < G.numVertexes; i++) {
        for (int j = i + 1; j < G.numVertexes; j++) {
            if (G.arc[i][j] != 0 && G.arc[i][j] < 65535) {
                edges[k].begin = i;
                edges[k].end = j;
                edges[k].weight = G.arc[i][j];
                k++;
            }
        }
    }

    // 边排序
    SortEdges(edges, G.numEdges);

    printf("最小生成树的边如下：\n");
    for (i = 0; i < G.numEdges; i++) {
        n = Find(&ds, edges[i].begin);
        m = Find(&ds, edges[i].end);
        if (n != m) {
            printf("(%d, %d) 权值: %d\n", edges[i].begin, edges[i].end, edges[i].weight);
            sum += edges[i].weight;
            Union(&ds, n, m);
        }
    }
    printf("最小生成树的总权值为: %d\n", sum);
}

// 示例主函数
int main() {
    MGraph G;
    int i, j;
    G.numVertexes = 6;
    G.numEdges = 9;
    int arc[6][6] = {
        {0, 6, 1, 5, 65535, 65535},
        {6, 0, 5, 65535, 3, 65535},
        {1, 5, 0, 5, 6, 4},
        {5, 65535, 5, 0, 65535, 2},
        {65535, 3, 6, 65535, 0, 6},
        {65535, 65535, 4, 2, 6, 0}
    };
    for (i = 0; i < G.numVertexes; i++)
        for (j = 0; j < G.numVertexes; j++)
            G.arc[i][j] = arc[i][j];

    Kruskal(G);
    return 0;
}

🌳最短路径

无向图 有向图都可以使用

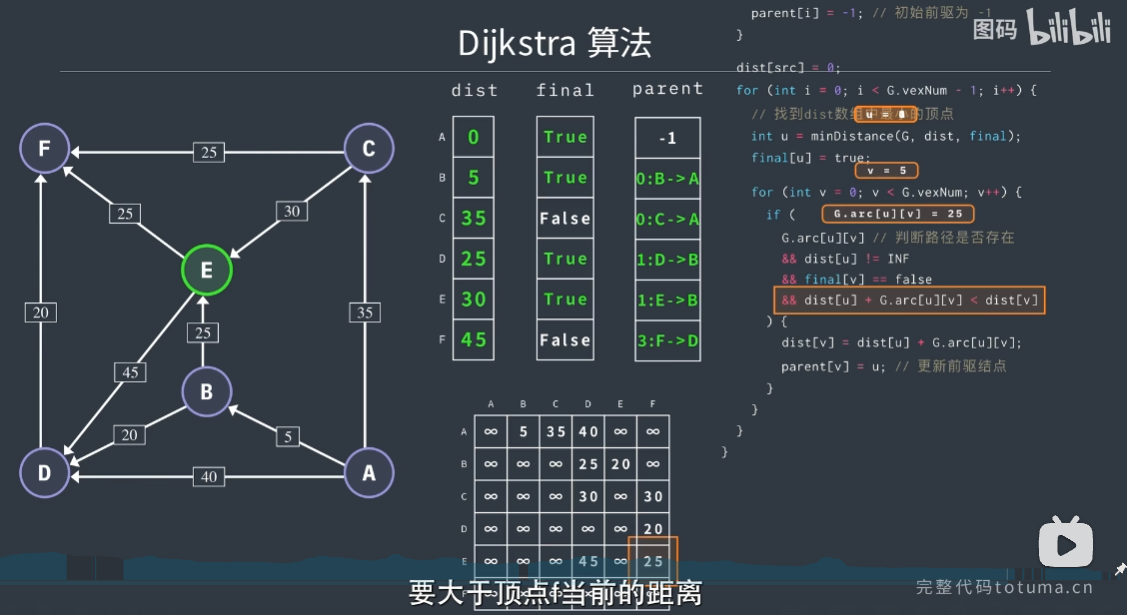
🌳dijkstra 算法

贪心算法

单源最短路径

dijkstra算法

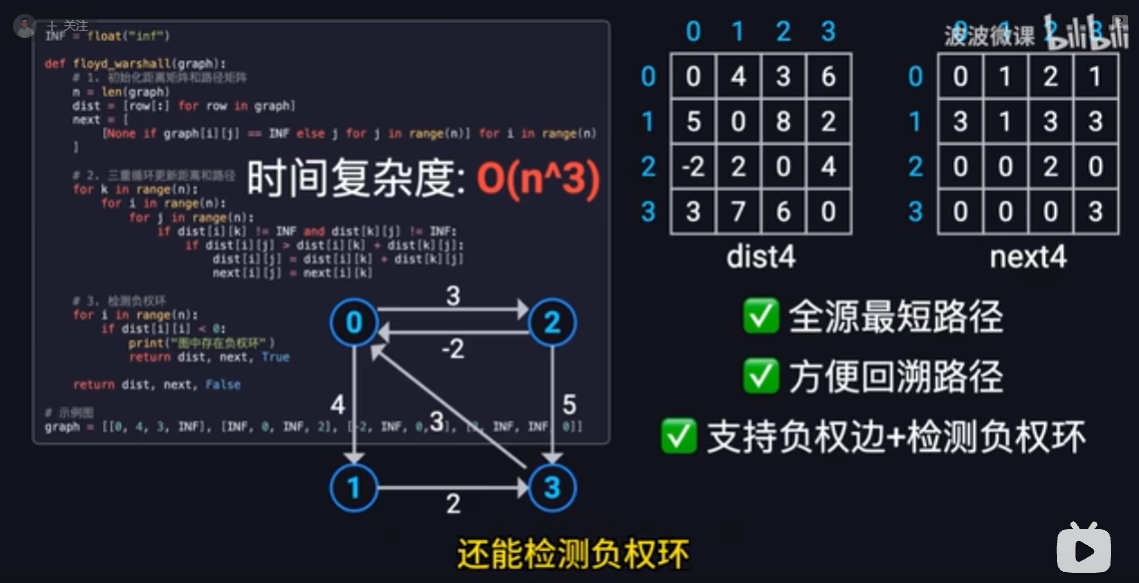
🌳floyd 算法

动态规划思路

全源最短路径

支持负权边
检测负权环

floyd算法

🌳拓扑排序 topological sorting

AOV 网 activity on vertex network：用顶点表示活动的网，有向边用来表示活动之间的先后顺序

拓扑排序：对AOV网工程活动的流程排序

DAG 有向无环图 Directed Acyclic Graph

拓扑排序可以用来检测有向图中是否有环路

拓扑排序序列不唯一

🌳关键路径

🌳8. 查找

🌳9. 排序

Here is a footnote reference,[^1] and another.[^longnote]

🌳Endnotes

[^1]: Here is the footnote.
[^longnote]: Here’s one with multiple blocks.